NEW POSITION
In 2011 I moved to a new position with the Visual Computing Group at Microsoft Research Asia. My new webpage can be found
here.
OLD WEBSITE
David Wipf
Postdoctoral Fellow
Biomagnetic Imaging Lab
University of California, San Francisco
513 Parnassus Avenue, S362
San Francisco, CA 94143
Email: {first name}.{last name} at gmail.com
Background and Research Interests
I recently completed my Ph.D. at the University of California, San Diego where I was an NSF Fellow in Vision and Learning in Humans and Machines. Now I am an NIH Postdoctoral Fellow at the University of California, San Francisco working on Bayesian estimation as applied to the problem of finding sparse representations of signals using overcomplete (redundant) dictionaries of candidate features. In contrast to the Moore-Penrose pseudoinverse, which produces a representation with minimal energy or high diversity, I'm concerned with finding inverse solutions using a minimum number of nonzero expansion coefficients (maximal sparsity). A particularly useful application of this methodology is to the source localization problem that arises in neuroelectromagnetic imaging and brain computer interfacing (BCI). Here the goal is to convert an array of scalp sensor measurements into an estimate of synchronous current activity within the brain which can then be used for classifying brain states or other clinical tasks. I'm also looking at sparse coding problems associated with the visual cortex.
Publications by Year
2010
- D.P. Wipf, B.D. Rao, and S. Nagarajan, ``Latent Variable Bayesian Models for Promoting Sparsity," IEEE Transactions on Information Theory (to appear). Download
- M. Seeger and D.P. Wipf, "Variational Bayesian Techniques for Sparse Inference and Estimation," IEEE Signal Processing Magazine (in press).
- R.R. Ramírez, D.P. Wipf, and S. Baillet, ``Neuroelectromagnetic Source Imaging of Brain Dynamics," W. Chaovalitwongse, P. Pardalos, and P. Xanthopoulos, editors, Computational Neuroscience, Springer (in press).
- D.P. Wipf and S. Nagarajan, ``Iterative Reweighted
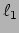 and
and 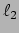 Methods for Finding Sparse Solutions," Journal of Selected Topics in Signal Processing (Special Issue on Compressive Sensing), vol. 4, no. 2, April 2010. Download
Methods for Finding Sparse Solutions," Journal of Selected Topics in Signal Processing (Special Issue on Compressive Sensing), vol. 4, no. 2, April 2010. Download
- D.P. Wipf, J.P. Owen, H.T. Attias, K. Sekihara, and S. Nagarajan, ``Robust Bayesian Estimation of the Location, Orientation, and Timecourse of Multiple Correlated Neural Sources using MEG," NeuroImage, vol. 49, no. 1, Jan 2010. Download
(Trainee Abstract Award, Human Brain Mapping 2009)
2009
- D.P. Wipf and S. Nagarajan, ``Sparse Estimation Using General Likelihoods and Non-Factorial Priors," Y. Bengio, D. Schuurmans, J. Lafferty, C. Williams and A. Culotta, editors, Advances in Neural Information Processing Systems 22, MIT Press, 2009. Download
- D.P. Wipf and S. Nagarajan, ``Solving Sparse Linear Inverse Problems: Analysis of Reweighted
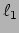 and
and 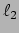 Methods," Workshop on Signal Processing with Adaptive Sparse Structured Representations, Saint-Malo, France, April 2009. Download
Methods," Workshop on Signal Processing with Adaptive Sparse Structured Representations, Saint-Malo, France, April 2009. Download
- D.P. Wipf, J.P. Owen, H.T. Attias, K. Sekihara, and S. Nagarajan, ``Estimating the Location and Orientation of Complex, Correlated Neural Activity using MEG," D. Koller, D. Schuurmans, Y. Bengio, and L. Bottou, editors, Advances in Neural Information Processing Systems 21, MIT Press, 2009. Download
- D.P. Wipf and S. Nagarajan, ``A Unified Bayesian Framework for MEG/EEG Source Imaging," NeuroImage, vol. 44, no. 3, February 2009. Download
(Young Investigator Award, Biomag 2008)
2008
- D.P. Wipf and S. Nagarajan, ``A New View of Automatic Relevance Determination," J.C. Platt, D. Koller, Y. Singer, and S. Roweis, editors, Advances in Neural Information Processing Systems 20, MIT Press, 2008. Download
2007
- D.P. Wipf and B.D. Rao, ``An Empirical Bayesian Strategy for Solving the
Simultaneous Sparse Approximation Problem," IEEE Transactions on
Signal Processing, vol. 55, no. 7, July 2007. Download
- D.P. Wipf and S. Nagarajan, ``Beamforming using the Relevance Vector Machine," International Conference on Machine Learning, June 2007. Download
- D.P. Wipf, J.A. Palmer, B.D. Rao, and K. Kreutz-Delgado,
``Performance Analysis of Latent Variable Models with Sparse Priors," IEEE International Conference on Acoustics,
Speech, and Signal Processing, Honolulu, USA, May 2007. Download
- D.P. Wipf, R.R. Ramírez, J.A. Palmer, S. Makeig, and B.D. Rao,
``Analysis of Empirical Bayesian Methods for Neuroelectromagnetic Source Localization,"
B. Schölkopf, J. Platt, and T. Hoffman, editors, Advances in Neural Information Processing Systems 19, MIT Press, 2007. Download
(Outstanding Student Paper Award)
2006
- D.P. Wipf, ``Bayesian Methods for Finding Sparse Representations," Ph.D. Thesis, UC San Diego, 2006. Download
- D.P. Wipf and B.D. Rao, ``Comparing the Effects of Different Weight
Distributions on Finding Sparse Representations," Y. Weiss, B. Schölkopf, and
J. Platt, editors, Advances in Neural Information Processing Systems 18, MIT
Press, 2006. Download
- J.A. Palmer, D.P. Wipf, K. Kreutz-Delgado, and B.D. Rao, ``Variational EM
Algorithms for Non-Gaussian Latent Variable Models," Y. Weiss, B. Schölkopf,
and J. Platt, editors, Advances in Neural Information Processing Systems 18,
MIT Press, 2006. Download
2005
- D.P. Wipf and B.D. Rao, ``Finding Sparse Representations in Multiple
Response Models via Bayesian Learning," Workshop on Signal Processing with
Adaptive Sparse Structured Representations, Rennes, France, November 2005. Download
- J. McCall, D. Wipf, M. Trivedi, and B. Rao, ``Lane Change Intent Analysis
Using Robust Operators and Sparse Bayesian Learning," IEEE International
Workshop on Machine Vision for Intelligent Vehicles, San Diego, USA, June 2005. Download
(Student Paper Award)
- D.P. Wipf and B.D. Rao, ``
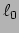 -Norm Minimization for Basis Selection,"
L. Saul, Y. Weiss, and L. Bottou, editors, Advances in Neural Information
Processing Systems 17, MIT Press, 2005. Download
-Norm Minimization for Basis Selection,"
L. Saul, Y. Weiss, and L. Bottou, editors, Advances in Neural Information
Processing Systems 17, MIT Press, 2005. Download
2004
- D.P. Wipf and B.D. Rao, ``Sparse Bayesian Learning for Basis Selection,"
IEEE Transactions on Signal Processing, vol. 52, No. 8, August 2004. Download
- D.P. Wipf and B.D. Rao, ``Probabilistic Analysis for Basis Selection via
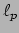 Diversity Measures," IEEE International Conference on Acoustics,
Speech, and Signal Processing, vol. 2, Montreal, Canada, May 2004. Download
Diversity Measures," IEEE International Conference on Acoustics,
Speech, and Signal Processing, vol. 2, Montreal, Canada, May 2004. Download
- D.P. Wipf, J.A. Palmer, and B.D. Rao, ``Perspectives on Sparse Bayesian
Learning," S. Thrun, L. Saul, and B. Schölkopf, editors, Advances in
Neural Information Processing Systems 16, MIT Press, 2004. Download
Matlab Code
Some of the algorithms we use can be run using a very simple Matlab code. Several generalized versions of SBL (popularly known as the relevance vector machine) are included as well as 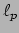 -norm minimization methods. All are (somewhat) optimized to work well with very overcomplete dictionaries (unlike some RVM code available elsewhere). In general, I have found that the slower EM updates sometimes give better solutions, but can be impractical to run for large problems. Regardless, the code here should work ok with many thousands of dictionary columns as long as the number of rows is small enough (e.g.
-norm minimization methods. All are (somewhat) optimized to work well with very overcomplete dictionaries (unlike some RVM code available elsewhere). In general, I have found that the slower EM updates sometimes give better solutions, but can be impractical to run for large problems. Regardless, the code here should work ok with many thousands of dictionary columns as long as the number of rows is small enough (e.g.
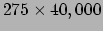 works fine with the fast updates, but is too slow for standard EM). Please send me an email if there are any problems. Note also that this code can be speeded up dramatically by removing the SVD computation which is not required but can be more numerically stable in some situations.
works fine with the fast updates, but is too slow for standard EM). Please send me an email if there are any problems. Note also that this code can be speeded up dramatically by removing the SVD computation which is not required but can be more numerically stable in some situations.
Download
Also, for a very fast implementation of SBL that uses the method of Tipping and Faul (2003), you can check here.
David Wipf
2010-09-10
![\begin{figure}
\centering\includegraphics[width=5in]{labpic.eps}
\end{figure}](Timg1.png)
![\begin{figure}
\centering\includegraphics[width=5in]{labpic.eps}
\end{figure}](Timg1.png)
![]() -norm minimization methods. All are (somewhat) optimized to work well with very overcomplete dictionaries (unlike some RVM code available elsewhere). In general, I have found that the slower EM updates sometimes give better solutions, but can be impractical to run for large problems. Regardless, the code here should work ok with many thousands of dictionary columns as long as the number of rows is small enough (e.g.
-norm minimization methods. All are (somewhat) optimized to work well with very overcomplete dictionaries (unlike some RVM code available elsewhere). In general, I have found that the slower EM updates sometimes give better solutions, but can be impractical to run for large problems. Regardless, the code here should work ok with many thousands of dictionary columns as long as the number of rows is small enough (e.g.
![]() works fine with the fast updates, but is too slow for standard EM). Please send me an email if there are any problems. Note also that this code can be speeded up dramatically by removing the SVD computation which is not required but can be more numerically stable in some situations.
works fine with the fast updates, but is too slow for standard EM). Please send me an email if there are any problems. Note also that this code can be speeded up dramatically by removing the SVD computation which is not required but can be more numerically stable in some situations.